Bible prophecies

In Mark 13, Jesus told 10 prophecies. I am going to use bayesian inference to

• test the hypothesis that prophecies in bible are fulfilled by chance \(H_0: p = 0.5\)
• predict the chance of these 10 prophecies to be fulfilled.

It is said that ~2500 prophecies were made in the bible and 2000 of them have been fulfilled (ref). Assuming prophecies are binomial trials (true or false only), in a bayesian approach, the equation for posterior distribution is:

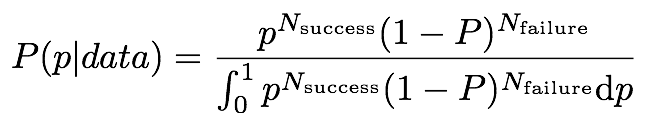
Assume those prophecies that are not fulfilled at this point as failure. So we have:

• N_success = 2000 and
• N_failure = 490. (removed the 10 prophecies in Mark 13)

As this denominator are not easily integrated in R, I was suggested to use the following algorithm using pdf of a beta distribution to get the probability of prophecies-fulfilled-probability (ref).

• iterating from 0 to 1 for generating the pdf curves for posterior distribution. Let prior be 1,
• iterating from 2000 (current fulfilled prophecies) to 2490 (all prophecies except the ones in Mark 13)

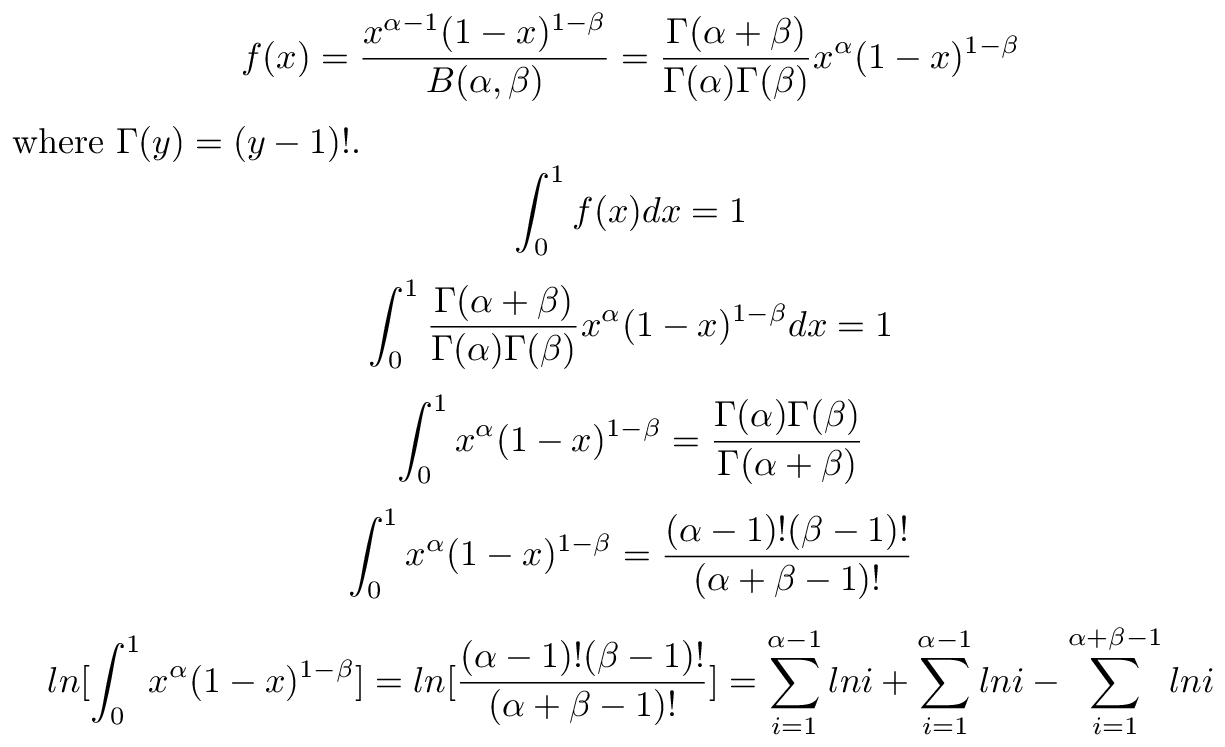
library(Rcpp)  
library(ggplot2)  
library(data.table)  

sourceCpp('/Users/wckdouglas/scripts/R/Rcpp/integral.cpp')
all = 2490
success = 2000
prob = seq(0,1,0.00005)
result = lapply(seq(success,all,80),function (x) return(data.table(probOfProb(prob,x,all-x),x,prob)))
result = data.table(do.call(rbind,result)) 
setnames(result,c('probofProb','success','prob'))
ggplot(data= result,
       aes(x=prob,y=probofProb,color=as.factor(success))) +
    labs(y = 'Probability of probabilty',
         x = 'Probability of confidency on bible prophecies',
         color='Fullfilled') +
    geom_point()

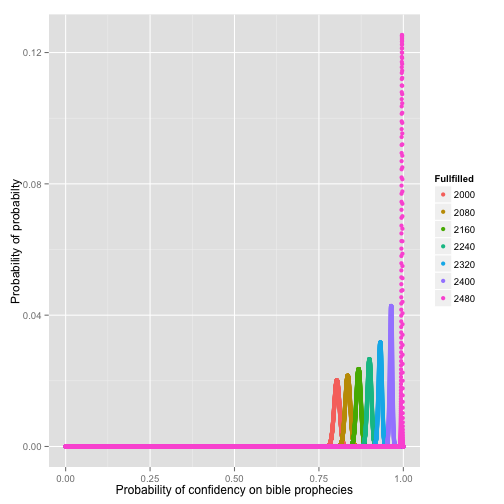
From the red curve (N_success=2000), getting the likelihood ratio between 0.8 and 0.5 (random).

likelihood_ratio = probOfProb(0.8,2000,500)/probOfProb(0.5,2000,500)
likelihood_ratio

## [1] 1.86192e+209

So it is 1.8619198 × 10²⁰⁹ more likely that prophecies in bible are not randomly fulfilled and keep in mind that the assumption was the other unfulfilled prophecies are not going to happen. It will go higher than 0.8 in the future (not as the curve shown, as prior changes).

In addition, this test assumes bible prophecies are bernoulli trials where the result can only be 1 or 0. A detailed accuracy test has been done in here.

And it is very likely that ~80% of chance that the prophecies in Mark 13 will be fulfilled!